AcouS PROPA calculation model

AcouS PROPA® simulates sound propagation due to one more sources of noise in open or closed 3D environments.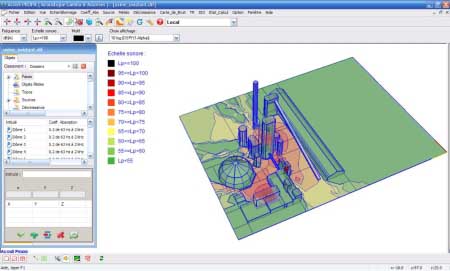

Diffuse reflectance model

This softawre is based on the assumption of acoustic diffuse reflection in a wall according to Lambert's law and assumes that the intensity at any point in the space consists of the superposition of a direct component, i.e. the intensity emitted directly by the source component and a reverberant. The first term, easily ascertainable, is a free-field propagation of spherical waves whose theoretical model is well known. On the other hand the second term is more difficult to quantify. It requires the assimilation of the walls of the premises in triangular surface elements behaving as point sources of well-defined directionality.

In addition, this model takes into account the geometry of the room, material characteristics and positions of the source and receiver.

This method chooses the descriptive variables as power densities (homogeneous intensity) present on the walls. The mathematical process that governs their determination is a process called "Markovian" which asserts that the state of a physical phenomenon depends only on its previous statements directly. Thus, in our case, the power density present on a dS' wall element at a t instant depends only on those present on all other e dS' elements forming the space at t instants diminished by  their travel time respectively.

The dS wall element behaves like a point source at its centroid. Its radiation is spherical and that in the upper half-space. Its directivity is of the form : Q (Ɵ) = 4 cos Ɵ

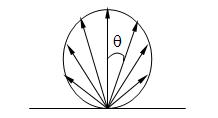
Before any acoustic simulation, a factor known as "shape" is computed and translated in the form of a matrix, the visibility between each sample of sides, or sources, or points of reception. This coefficient depends only on the number of samples and therefore the number of wall and surface samples.

Then from the characteristics of the noise source (power per band, directivity, position), the algorithm performs a complete energy balance between the samples and determines the power density received by each of them compared to others and the direct wave. This calculation obviously takes into account the absorption of the walls of the premises.

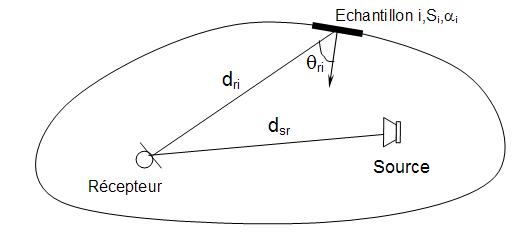
The intensity received at the receiving point then has two components. The first corresponds to the intensity direct from the source whose propagation is in free field and the second comes from the different surface elements dS involved in the process of diffuse reflection.

AcouS PROPA® acoustic software was developed on this model of diffuse reflection over the past twenty years and has been compared to measurements on several occasions with convincing results.

Model taking into account the diffraction

Taking into account the phenomenon of diffraction is a key element and not negligible, especially in open spaces. The algorithm is based on the theory of Maekawa.

Before any calculation af attenuation for a given source and receiver, the algorithm fills in the form factor of all possible paths between each source element, each "free" edge of the premises and each receiving element. The calculated routes are considered the shortest between each of these elements. For a given receiver, the algorithm then calculates the total attenuation provided by each of these routes. This attenuation is then subtracted at direct pressure to get the "diffracted" level received.